Gary Rubinstein's Blog: The Missed Opportunity Myth
Before Michelle Rhee was a board member for Miracle-Gro she was the founder and CEO of StudentsFirst. Before that, she was Chancellor of Washington D.C. schools from 2007 to 2010. Before that, she was the CEO of The New Teacher Project.
And even though Rhee is not a public figure anymore in education, she continues to influence education policy through The New Teacher Project which has since changed its name to TNTP. TNTP puts out slick papers that it calls research but is really propaganda disguised as research. Their first one was called ‘The Widget Effect’ which laid out the case for replacing salary schedules with a system based on merit pay based on statistically inappropriate analysis of standardized test scores.
And over the years they have put out other papers with clever titles like ‘The Irreplaceables’, ‘Rebalancing Teacher Tenure’, and ‘Teacher Evaluation 2.0.’ These papers are often quoted by ed reform propaganda sites like The74 and Education Post.
One of their most recent papers is called ‘The Opportunity Myth.’ Its central thesis is something that reformers love to use in their teacher bashing arguments, which is that too many teachers shortchange their students by having low expectations for them. The work they assign is not challenging enough and since students always rise to the challenge of whatever you assign to them, these teachers are negligent in their duties.
So TNTP observed 1,000 lessons in five school districts and analyzed 5,000 assignments and 20,000 student work samples. They concluded that the work that the students were assigned was usually inappropriate for their grade level. Here is one of their graphics from the paper.

So 75% of the time students are working on things “that were not grade appropriate.”
My first question about this study is: If a teacher is teaching a 5th grade class where the students are behind and only at a 3rd grade reading level, but you give them material at a 4th grade level, are you someone with low expectations or high expectations? I would say you are someone with high expectations. But this research paper would conclude that this teacher was someone with low expectations because the 4th grade reading level is lower than the grade the students are in. This is the main flaw with the misleading conclusion so happily quoted by the reform propaganda sites.
TNTP actually put up samples of the assignments they rated on their website so I took a look at how they rated some math assignments to see if I agreed with their ratings. I was not surprised to see that when it came to 8th grade math, the TNTP raters had no idea what they were talking about.
This part is a bit ‘mathy’ but I will do my best to explain the context of this assignment so if you are not a math teacher you can still get the idea of how misguided TNTP is in their rating system.
One of the most important concepts is math is something called ‘slope.’ It is first taught in 7th or 8th grade and it is weaved into all the following courses and actually comprises a large part of Calculus. Informally speaking, the slope of a line is a measure of how steep it is.
In the picture below, the segment AB has a slope of 1, the segment CD has a slope of 2, and the segment EF has a slope of 1/2.
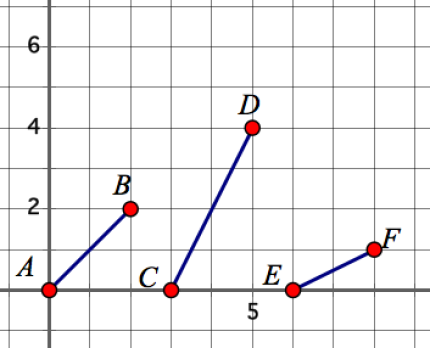
A slope of 2 means that for every unit you move to the right, you have to move up 2 units. For segment CD, to get from C to D you would move two units right and four units up. So if you only moved one unit to the right from C, you would move two units up to get to the point on the line.
One of the main ways of testing to see if students know slope is to give a diagram with a line segment on it and ask them to compute the slope.

The slope of this line segment is:
A) 1/3 B) 3 C) -1/3 D) -3 E) Slope is not a ‘thing’
If you said ‘B’, you are correct. To get from (2,1) to (5,10) you have to go three units to the right and nine units up. So if you only went one unit to the right, you would only go three units up.
There is also a ‘formula’ for slope:

There are a lot of way to test to see if a student understands the concept of slope. If you just have the students calculate slope over and over there is a chance they they don’t really ‘understand’ slope but that they just memorized a formula. Still, if you have a student who cannot calculate the slope of a line or line segment when the coordinates of two points are known, then that student surely does not understand the concept of slope.
Now (and I know I’m losing readers here by the minute — but you have to have some background so you can understand why I contend that TNTP is not qualified to judge the quality of a math assignment based on a lesson about slope) you may not be surprised that if there are three points on the same line segment and if you calculated the slope by picking any pair of those points, you would get the same answer. In this case, you will get a slope of three no matter which two points you choose.

Informally speaking, if the slope of the segment from (2,1) to (4,7) was different from the slope of the segment from (4,7) to (5,10) then it wouldn’t be a straight line.
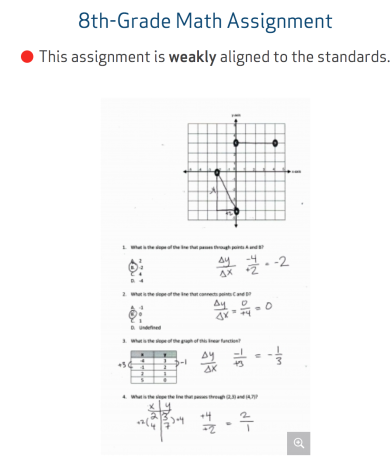
When you go to the TNTP page where they show examples of activities and how they rated them, they have this example for a lesson about slope.

Math teachers I’m sure will agree that this is a good set of questions. The first two questions are based on a graph and the student knew to draw a vertical and horizontal line which shows a conceptual understanding beyond just plugging numbers into a formula. In the third question, the data is presented as a chart instead of on a graph, giving an opportunity for students to get comfortable with multiple representations and this question has six different ways to calculate the slope so there is opportunity for students to discuss that. In the fourth question the student creates a chart from the data and then does it like the third question. One of the answers is a positive integer, one is zero, one is a negative fraction, and one is a positive fraction so all different sorts of answers are covered. This is a fine example of practicing the skill of calculating the slope as data is presented in different ways.
But according to the ‘experts’ at TNTP, the teacher who created this assignment was guilty of low expectations.
TNTP explains why they made this judgement, but to understand why their rationale is nonsense, I’m going to have to take you through some more background about math and about the common core standards.
There are math standards from K to 8th grade and then standards for six different aspects of high school math. The math standards for a grade, like 8th grade, are pretty short, taking up maybe 10 pages if you print them out. States will take those standards and turn them into lesson maps where there will be 150 or so subtopics based on the standards. The standards are not very thorough, actually. There are big gaps in them that anyone who is a practicing math teacher would know need to be filled in.
So for 8th grade math, the concept of slope is only mentioned twice. Here is the text from the two mentions:

So there is no mention in the standards at all of mastering the skill of actually using the slope formula to calculate the slope of a line defined by data in various representations. Any real teacher would know that this is an extremely important skill that you would spend several days on as it will come up for the next 4 years in many important math units including several months of Calculus. And the teacher who made this assignment that was deemed ‘weakly’ aligned to the standards was aware that it would be negligent not so spend some time practicing with the slope formula.
So the TNTP people gave this explanation for why this was ‘weakly aligned’:

OK, so you likely have not been teaching math for 27 years like me so this explanation does look like something that they put a lot of thought into. So I’m going to say a few things about their rationale for bashing this assignment.
First of all, this is not the standard that the assignment was trying to address. This assignment is addressing a standard that is not explicitly stated because it is so obvious to everyone (except the TNTP raters) who needs to understand what sorts of things are needed in teaching the concept of slope.
Secondly, this standard 8.EE.B.6 is perhaps the most unnecessary and, sorry to use this language, stupidest standard I can imagine for this topic. Remember this picture I put up before?

They are saying that a better way to justify that if you have a straight line then the slope of any segment on that line will have the same slope is to apply a much more difficult concept to master from Geometry, the idea of similar triangles.
Similar triangles are two triangles where one is like a ‘zoomed in’ version of the other. So they are not necessarily congruent triangles because there is a little one and a big one. What makes them similar is that they have the same angle measurements.
So these two triangles are similar since they both have angles of about 72 degrees, 90 degrees, and about 18 degrees.

Notice that the sides of the big triangle are double the sides of the smaller triangle. We say that the corresponding sides are in proportion and this will always happen with similar triangles. It also works the other way around — if we know the corresponding sides are in proportion, then the triangles are similar so all their angles will be equal.
Using this concept of similar triangles, we can look at that straight line problem with three points on it in a different way (though this would not be advised since it is unnecessarily confusing and really won’t offer any truly useful insight into this topic at this point in 8th grade).

Adding some lines to make two triangles, you’ve got the big one with a horizontal side of 2 and a vertical side of 4 and you’ve got the small one with a horizontal side of 1 and a vertical side of 2. You also have that right angle in the bottom right corner of the triangle. If two sides are in proportion and the angle between those two sides is the same then these are similar triangles. And if they are similar triangles, the angles BAC and ECF would need to be the same too and if those angles are the same then the line ACF would have to be a straight line.
This is not something I would ever teach to 8th graders unless my principal said that I’ll get fired for not following the common core standards like they are the ten commandments. It is maybe an interesting curiosity that I could mention or not mention, depending on the situation. It certainly doesn’t belong on a short list of standards, like the common core standards. And for TNTP to pan this assignment because they don’t understand that a good teacher knows it would be negligent to try to push this ill advised standard if they can avoid it, and that a good teacher knows that even though it doesn’t say that the slope formula is something that should be practiced, it certainly is something that should.
I can probably do a similar analysis for every assignment that TNTP said is weakly aligned to the standards, but I won’t torture myself or the people who like to read this blog with any more of this.
TNTP is the legacy of Michelle Rhee. She, a bit like Voldemort in the early Harry Potter books, is out of sight right now but she continues to influence education policy through her intermediates and it is important to show that making a fancy paper that looks like real research and is quoted by The74, Education Post, and the TFA blog does not mean that the researchers are qualified to analyze the data they collect.
This blog post has been shared by permission from the author.
Readers wishing to comment on the content are encouraged to do so via the link to the original post.
Find the original post here:
The views expressed by the blogger are not necessarily those of NEPC.
